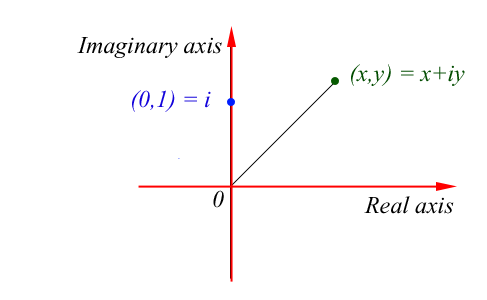Quaternions and the United Nations

Last week, I was doing my final long run before the upcoming Dublin marathon. On long runs, I generally like to take my stopwatch and run for a certain length of time, rather than for a certain number of miles. So today I aimed for three hours.

My brother Aidan came out with me to do a shorter run, and the chatting and laughing made the first hour pass very quickly. We did a loop so that he could return home easily (he's just come up from home to live in town and the possiblilities for getting lost are many). Now alone, I took a journey around the woodland tracks of the Phoenix Park (Europe's largest city park), before joining the Royal Canal at Ashtown and heading towards the sea.

Whilst running it occured to me that I should soon be running under Brougham Bridge, a quaint stone bridge that I'd heard quite a lot about in my undergraduate days studying theoretical physics at Trinity, in connection with a certain William Rowan Hamilton.

Hamilton was born in 1805 and quickly marked himself out as a child prodigy; at the age of 13 he had mastered Hebrew, Arabic, Sanskrit and Hindi (as well all the classical and modern European languages expected of any child prodigy worth his salt). His mathematics education was largely self-taught, and Trinity recognised his achievements by appointing him to a professorship at the age of 22, when he had not even completed his university studies.

Hamilton's most famed achievement is the discovery of quaternions. Those of you who didn't drop out of maths at the earlies legally allowable stage will probably have come across imaginary numbers at some stage. If you did drop out, then grab a calculator, type in -1 and press the square root sign, whereupon your calculator should start vehemently protesting. Why? Because the square root of -1 cant be written as a number. So what?, you might ask. Well that also means equations like

x 2 + 1 = 0

dont have any solution. Unless we make up a whole batch of new numbers, that is. And that's precisely what was done: We let the square root of -1 be equal to i, a so-called imaginary number. These imaginary numbers tend to crop up at an alarming rate when doing calculations in physics and engineering; however, they always manage to get out of the way just before any answers pertaining to the real world are obtained.

Back to our friend Hamilton. From primary school you'll remember we could put all numbers on a numberline (Im assuming none of you dropped out then!). However, imaginary numbers don't fit on this line and need one of their own. If you put the imaginary line at a 90 degree angle to the real one you get something that looks a bit like a 2D graph (called an Argand diagram) upon which you can plot any combination of real and imaginary numbers.

This set Hamilton thinking as to whether he could extrapolate this to three dimensions; this would mean creating another number, j, with its own numberline 90 degrees to the first two. This actually proved to be a bit of a problem.

I remember writing an article about how on many occasions great scientists have striven to the end of their tether for an answer to the problem they were working on and how the answer just came to them whilst they were doing something comparatively innocuous. This was especially true in this case. Hamilton kept notoriously long hours working on his problems; however one day , he was walking along the Royal Canal with his wife on his way to Dunsink observatory, where he was based. As he passed under the bridge, a flash of inspiration came to him. He wasn't able to extrapolate to three dimensions (later mathematicians showed this to be impossible) but he could extrapolate to four. According to legend, Hamilton took out his pocketknife and scratched out the formulae which numbers on the four numberlines (i, j, k, 1) would have to obey:

i 2 = j 2 = k 2 = ijk = -1

The formula is not to be seen on the bridge (indeed it would be hard to make it out under all the graffiti), but the obligatory plaque has been put up. The bridge has become kind of a place of pilgrimage, and in my PhD days it wasnt unusual to overhear a visiting mathematician asking directions to get there.

A major conceptual breakthrough was the fact that none of these numbers commuted when you multiplied them. Normally, if we have two numbers a and b then we take it for granted that ab=ba. However in the case of quaternions we get

ij= -ji

kj=-jk

ik= -ki

This was to prove an important conceptual stepping stone in the path to quantum mechanics, where data such as the position and energy of a particle are found by applying things called matrices which sometimes don't commute either. This non-commuting quantity is responsible for the famous Heisenberg uncertainty principle; you can't find out the exact position and energy of very small objects at the same time because their matrices don't commute. Indeed, there are enough of Hamilton's writings to suggest that had he been around in the 1920's when quantum mechanics were being developed, he could very well have played a significant role in its development. As for quaternions, they are still being used today in such diverse fields as computer game design and spacecraft control.

Out of interest, you can also extrapolate to eight dimensions (octonions) and sixteen dimensions (sedenions), indeed to any power of two, but it all gets very messy very quickly.

My run took me past the bridge at the 1:50 mark and again at the 2:20 mark. I've become very fond of the Royal Canal as a running route (although I usually go the other way, inland towards Clonsilla and Leixlip). I returned home via Stoneybatter, one of the last remaining parts of 'old' Dublin, where you can still smell turf fires burning. Irish and United Nations flags towered above a memorial to the Irish soilders who lost their lives serving in the Lebanon. The solitary figure mowing the lawn, is not quite so elderly as to make me wonder if perhaps he served in the Lebanon himself. The words 'United Nations' still evoke some higher ideal within, some vision of how things could be, which years of exposure to the crassness of international politics has not yet dimmed. I think of Uruguyan and Bangladeshi peacekeepers in the rain forests of the Congo, Ghanaians and Indians in the Lebanon, and I cannot think that they are there solely out o their governments' self-interest. My meditation teacher, Sri Chinmoy, has written many times of the United Nations. Here are some extracts from his book A Real Member of the United Nations, written in 1989:

A real member of the United Nations is he who claims the United Nations to be his own, very own. Unless and until he claims the United Nations to be his own, he will not be richly inspired to change its face and fate lovingly and surprisingly for the better.

A real member of the United Nations carries in his heart-pocket a valid visa to humanity's oneness-heart.

A real member of the United Nations does not expect the complete cure of world maladies by a 44-year-old United Nations. Countless problems were born long before it was born. Slow and steady wins the race. Let us hope for the best. Let us fervently hope that the world of peace the United Nations envisages will without fail be manifested on earth.

A real member of the United Nations forgives the United Nations mistakes, for he knows that the United Nations has been in existence for only 44 years. He hopes that in the forthcoming endless days the United Nations will not only rectify all its mistakes but also become the embodiment of truth-perfection.

Related Links: